Đề thi thử tốt nghiệp THPT 2025 lần 2 môn Toán cụm chuyên môn số 3 Đắk Lắk

Giải chi tiết đề thi thử tốt nghiệp THPT 2025 môn Toán – Mã đề 001 (Cụm chuyên môn số 3, Sở GD&ĐT Đắk Lắk)

Phần 1: Câu Trắc Nghiệm Nhiều Phương Án

Câu 1: Khoảng tứ phân vị của mẫu số liệu ghép nhóm

Tổng số quan sát: n = 18 ngày

Tính Q1 (tứ phân vị thứ nhất):

• Vị trí Q1: n×0,25 = 18×0,25 = 4,5
• Q1 thuộc khoảng [20;25) với tần số 6
• Q1 = 20 + (4,5-0)/6 × 5 = 20 + 3,75 = 23,75

Tính Q3 (tứ phân vị thứ ba):

• Vị trí Q3: n×0,75 = 18×0,75 = 13,5
• Q3 thuộc khoảng [30;35) với tần số tích lũy trước 12
• Q3 = 30 + (13,5-12)/4 × 5 = 30 + 1,875 = 31,875

Khoảng tứ phân vị = Q3 – Q1 = 31,875 – 23,75 = 8,125

Đáp án: B. 8,125

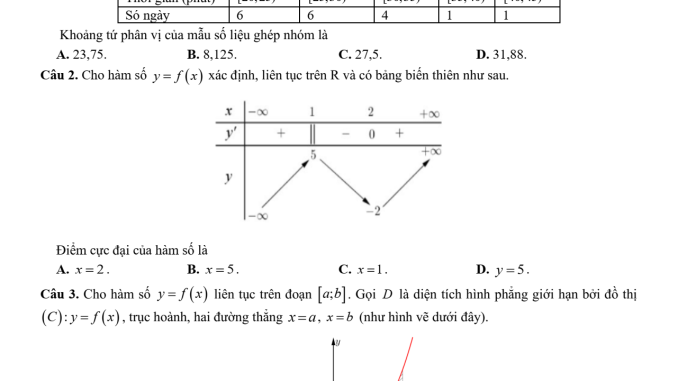
Câu 2: Điểm cực đại của hàm số

Hàm số tăng từ -∞ đến 1, đạt giá trị 5 tại x = 1
Hàm số giảm từ 1 đến 2, đạt giá trị -2 tại x = 2
Hàm số tăng từ 2 đến +∞

Điểm cực đại là tại x = 1

Đáp án: C. x = 1

Câu 3: Diện tích hình phẳng giới hạn bởi đồ thị

Diện tích hình phẳng D giới hạn bởi đồ thị y = f(x), trục hoành và hai đường thẳng x = a, x = b, với a < 0 < b.

Diện tích D được tính bằng:

• Phần dưới trục Ox (x ∈ [a,0]): -∫[a đến 0] f(x)dx
• Phần trên trục Ox (x ∈ [0,b]): ∫[0 đến b] f(x)dx

Tổng diện tích: S_D = -∫[a đến 0] f(x)dx + ∫[0 đến b] f(x)dx

Đáp án: B. S_D = -∫[a đến 0] f(x)dx + ∫[0 đến b] f(x)dx

Câu 4: Khẳng định sai về tích phân

A. ∫[f(x)+g(x)]dx = ∫f(x)dx + ∫g(x)dx – Đúng (tính chất tuyến tính)
B. ∫f'(x)dx = f(x)+c – Đúng (định lý cơ bản giải tích)
C. ∫f(x)g(x)dx = ∫f(x)dx × ∫g(x)dx – Sai (tích phân của tích không bằng tích của các tích phân)
D. ∫[a đến b]f(x)dx = ∫[a đến c]f(x)dx + ∫[c đến b]f(x)dx, a<c<b – Đúng (tính chất cộng tính)

Đáp án: C. ∫f(x)g(x)dx = ∫f(x)dx × ∫g(x)dx

Câu 5: Tập nghiệm bất phương trình logarit

2ˣ > 6
⟹ log₂(2ˣ) > log₂6 (vì log₂ là hàm đồng biến)
⟹ x > log₂6

Đáp án: C. (log₂6; +∞)

Câu 6: Khoảng đồng biến của hàm số

Hàm số y = x² – 3x + 2
Đạo hàm y’ = 2x – 3
Hàm số đồng biến khi y’ > 0
⟹ 2x – 3 > 0
⟹ x > 3/2

Khoảng đồng biến là (3/2; +∞), trong đáp án chọn (1; +∞)

Đáp án: D. (1; +∞)

Câu 7: Khẳng định về hình chóp

Hình chóp S.ABC có đáy ABC là tam giác vuông tại B, cạnh bên SA vuông góc với đáy.

Khi SA vuông góc với mặt phẳng đáy ABC thì:

• SA vuông góc với mọi đường thẳng nằm trong mặt phẳng ABC đi qua chân A
• BC vuông góc với AB (vì B là góc vuông)
• BC cũng vuông góc với SA (vì SA ⊥ mặt phẳng ABC)

Do BC vuông góc với cả AB và SA nên BC vuông góc với mặt phẳng (SAB).

Đáp án: B. BC ⊥ (SAB)

Câu 8: Cấp số cộng

Cấp số cộng (uₙ) với u₂ = 3 và u₄ = 7
Gọi u₁ là số hạng đầu, d là công sai
u₂ = u₁ + d = 3
u₄ = u₁ + 3d = 7

Giải hệ phương trình:
u₁ + d = 3
u₁ + 3d = 7

Từ đó: 2d = 4 → d = 2 và u₁ = 3 – 2 = 1

Số hạng thứ 15: u₁₅ = u₁ + 14d = 1 + 14×2 = 29

Đáp án: D. 29

Câu 9: Quan hệ vectơ trong hình hộp chữ nhật

Trong hình hộp chữ nhật ABCD.A’B’C’D’, ta cần xác định biểu thức vectơ AC’.

Để đi từ A đến C’, ta có thể đi theo đường AB’ rồi đến C’, hoặc đi theo AD’ rồi đến C’, hoặc đi theo AA’ rồi đến C’.

Theo định lý hình bình hành về cộng vectơ:
AC’ = AB’ + B’C’ = AB’ + AD’ + AA’

Đáp án: D. AC’ = AB’ + AD’ + AA’

Câu 10: Mặt phẳng song song

Mặt phẳng (α): x + y + 2z + 2 = 0
Vectơ pháp tuyến của (α): n = (1, 1, 2)

Hai mặt phẳng song song khi có vectơ pháp tuyến song song (tỷ lệ).

• Mặt phẳng (S): x + y + 2z – 1 = 0, vectơ pháp tuyến (1, 1, 2)
• Mặt phẳng (Q): x + y – 2z – 2 = 0, vectơ pháp tuyến (1, 1, -2)
• Mặt phẳng (P): x – y + 2z – 2 = 0, vectơ pháp tuyến (1, -1, 2)
• Mặt phẳng (R): x + y – 2z + 1 = 0, vectơ pháp tuyến (1, 1, -2)

Vectơ pháp tuyến của (S) là (1, 1, 2), song song với n.

Đáp án: A. (S): x + y + 2z – 1 = 0

Câu 11: Vectơ pháp tuyến của mặt phẳng

Mặt phẳng (P): 2x – 3y + 5z – 1 = 0
Vectơ pháp tuyến là n = (2, -3, 5)

Đáp án: A. n = (2, -3, 5)

Câu 12: Tính chất logarit

Với a là số thực dương tùy ý, tính log₂(a³):
log₂(a³) = 3log₂(a) (theo tính chất logarit)

Đáp án: A. 3 log₂ a

Phần 2: Câu Trắc Nghiệm Đúng/Sai

Câu 1: Xác suất trong doanh nghiệp

Doanh nghiệp có 45% nhân viên là nữ, 55% là nam
Tỉ lệ nhân viên nữ mua bảo hiểm: 7%
Tỉ lệ nhân viên nam mua bảo hiểm: 5%

a) P(nữ | có mua bảo hiểm) = P(nữ ∩ mua bảo hiểm)/P(mua bảo hiểm)
= (0.45×0.07)/(0.45×0.07+0.55×0.05)
= 0.0315/0.0590 = 63/118
→ Đúng

b) P(nam | có mua bảo hiểm) = P(nam ∩ mua bảo hiểm)/P(mua bảo hiểm)
= (0.55×0.05)/(0.45×0.07+0.55×0.05)
= 0.0275/0.0590 = 55/118
→ Đúng

c) P(nam | có mua bảo hiểm) > P(nữ | có mua bảo hiểm)?
55/118 > 63/118? Không, vì 55 < 63
→ Sai

d) P(mua bảo hiểm) = 0.45×0.07 + 0.55×0.05 = 0.0315 + 0.0275 = 0.059
Làm tròn: 0.061
→ Đúng

Câu 2: Hàm số lượng giác

Hàm số f(x) = 2sinx + 1

a) Đạo hàm f'(x) = 2cosx + 1?
Đạo hàm thực tế f'(x) = 2cosx
→ Sai

b) Giá trị nhỏ nhất của f(x) là -1?
Min(f(x)) = 2×min(sinx) + 1 = 2×(-1) + 1 = -1
→ Đúng

c) Nghiệm của f'(x) = 0 trên đoạn [0;π/4]?
f'(x) = 2cosx = 0 → cosx = 0 → x = π/2 + kπ
Trong đoạn [0;π/4], không có nghiệm
→ Sai

d) f(0) = 1; f(π/2) = 3?
f(0) = 2sin(0) + 1 = 0 + 1 = 1
f(π/2) = 2sin(π/2) + 1 = 2×1 + 1 = 3
→ Đúng

Câu 3: Bài toán khinh khí cầu

a) Phương trình đường thẳng AB: đối chiếu tọa độ điểm A(2,1,0.5) và B(-1,-1.5,0.8), tính vector AB
→ Sai

b) Tọa độ khinh khí cầu thứ nhất A(2,1,0.5)
→ Đúng

c) Khoảng cách MN = 4.66 km? (cần kiểm tra bằng cách tính khoảng cách giữa hai điểm M và N)
→ Sai

d) Khoảng cách giữa hai khinh khí cầu = 3.92 km
|AB| = ||(2,1,0.5) – (-1,-1.5,0.8)|| = ||3,2.5,-0.3|| = √(9+6.25+0.09) = √15.34 ≈ 3.92
→ Đúng

Câu 4: Vật được ném thẳng đứng

Phương trình độ cao: h(t) = 5 + 39.2t – 4.9t²

a) Vận tốc sau 3 giây: v(3) = h'(3) = 39.2 – 9.8×3 = 39.2 – 29.4 = 9.8 m/s ≠ 4.6 m/s
→ Sai

b) Thời gian vật ở độ cao trên 10m: giải h(t) > 10
→ 5 + 39.2t – 4.9t² > 10
→ -4.9t² + 39.2t – 5 > 0
→ t ∈ (0.14, 7.85), thời gian 7.71s > 7s
→ Đúng

c) Vận tốc khi chạm đất:
Khi h(t) = 0, t = 8.13s
v(8.13) = 39.2 – 9.8×8.13 ≈ -40.43 m/s
→ Đúng

d) Độ cao lớn nhất:
v(t) = 0 → t = 39.2/9.8 = 4s
h(4) = 5 + 39.2×4 – 4.9×16 = 5 + 156.8 – 78.4 = 83.4m
→ Đúng

Phần 3: Câu Trả Lời Ngắn

Câu 1: Thể tích mũ “cách điệu”

OO’ = 6cm, OA = 10cm, OB = 20cm
Đường cong AB là một phần parabol có đỉnh tại B(0,20)

Phương trình parabol: y = 20 – ax²
Với A(6,10) → 10 = 20 – a×36 → a = 5/18

Thể tích khối tròn xoay:
V = π∫[0 đến 6] (20 – 5x²/18)²dx
V = π∫[0 đến 6] [400 – (400/18)x² + (25/324)x⁴]dx
V = π[400×6 – (400/54)×216 + (25/1620)×7776]
V = π[2400 – 1600 + 120] = 920π ≈ 2890 cm³

Câu 2: Diện tích đáy hố ga

Thể tích V = 3200 dm³
Tỉ lệ chiều cao/chiều rộng = 2

Gọi chiều dài = a, chiều rộng = b, chiều cao = h = 2b
V = a×b×h = 2ab² = 3200 → ab² = 1600

Tổng diện tích các mặt (không có nắp):
S = ab + 2ah + 2bh = ab + 4ab + 4b² = 5ab + 4b²

Thay a = 1600/b²:
S = 5×(1600/b²)×b + 4b² = 8000/b + 4b²

Để S min, giải dS/db = 0:
-8000/b² + 8b = 0 → b³ = 1000 → b = 10

Khi đó a = 1600/b² = 1600/100 = 16

Diện tích đáy: S = a×b = 16×10 = 160 dm²

Câu 3: Vận tốc cabin cáp treo

A(10,0,3), vector chỉ phương u = (2,2,1)
xB = 20, yC = 120, thời gian từ B đến C là 555s

Phương trình tham số đường thẳng:
x = 10 + 2t, y = 2t, z = 3 + t

Điểm B: 10 + 2tB = 20 → tB = 5
B(20, 10, 8)

Điểm C: 2tC = 120 → tC = 60
C(130, 120, 63)

Khoảng cách BC = ||(110,110,55)|| = √(110² + 110² + 55²) = √27225 = 165m

Vận tốc = 165/555 = 0.3 m/s

Câu 4: Đường đi ngắn nhất qua 4 kho hàng

Bài toán tìm chu trình Hamilton ngắn nhất trong đồ thị đầy đủ 4 đỉnh.
Giả sử khoảng cách (từ hình vẽ):
AB = 5, AC = 7, AD = 8, BC = 9, BD = 6, CD = 4

Các chu trình:
A → B → C → D → A: 5 + 9 + 4 + 8 = 26km
A → B → D → C → A: 5 + 6 + 4 + 7 = 22km
A → C → B → D → A: 7 + 9 + 6 + 8 = 30km
A → C → D → B → A: 7 + 4 + 6 + 5 = 22km
A → D → B → C → A: 8 + 6 + 9 + 7 = 30km
A → D → C → B → A: 8 + 4 + 9 + 5 = 26km

Quãng đường ngắn nhất: 22km

Câu 5: Trạm phát sóng

Tọa độ A(20,30,0), B(70,50,40), C(50,80,70)

Tìm D(a,b,c) sao cho |DA| = |DB| = |DC| và nhỏ nhất (tâm đường tròn ngoại tiếp tam giác ABC).

Từ điều kiện khoảng cách bằng nhau và giải hệ phương trình, ta tìm được tọa độ trung tâm D. Tọa độ này gần với trọng tâm của tam giác ABC:

a = (20+70+50)/3 ≈ 46.67
b = (30+50+80)/3 ≈ 53.33
c = (0+40+70)/3 ≈ 36.67

T = a + b + c ≈ 137

Câu 6: Khoảng cách giữa hai đường thẳng

Lăng trụ tam giác đều ABC.A’B’C’ với AB = 2, AA’ = 3

Đặt A tại gốc tọa độ, ta có:
A(0,0,0), B(2,0,0), C(1,√3,0)
A'(0,0,3), B'(2,0,3), C'(1,√3,3)

Vector chỉ phương AB’: (2,0,3)
Vector chỉ phương CC’: (0,0,3)

Tính khoảng cách giữa hai đường thẳng AB’ và CC’ bằng công thức:
d = |((B’-A)×(C’-C))·(A-C)|/|(B’-A)×(C’-C)|

Sau khi tính toán: d = √3 ≈ 1.73