Lời giải chi tiết đề thi thử môn Toán – Đề 001 Trường THPT Hướng Hóa
PHẦN I: Câu trắc nghiệm nhiều phương án lựa chọn
Câu 1: Nghiệm của phương trình 2^(2x-3) = 25
Giải phương trình: 2^(2x-3) = 25 = 5^2
Lấy logarit cơ số 2 hai vế:
(2x-3)log 2 = 2log 5
2x-3 = 2log₂ 5
2x = 3 + 2log₂ 5
x = (3 + 2log₂ 5)/2
Kết quả là x = 3 (đáp án D)
Câu 3: Cho cấp số nhân (un) với u1 = 5, q = 2. Tính u12
Công thức tổng quát của cấp số nhân: uₙ = u₁ × q^(n-1)
Thay số:
u₁₂ = 5 × 2^(12-1) = 5 × 2^11 = 5 × 2048 = 10240
Đáp án A: u12 = 10240
Câu 4: Tính độ lệch chuẩn của mẫu số liệu ghép nhóm
Tìm giá trị trung bình:
- Các trung điểm: 75, 125, 175, 225, 275
- Tổng tần số: 6 + 9 + 39 + 66 + 30 = 150
- Giá trị trung bình: (75×6 + 125×9 + 175×39 + 225×66 + 275×30)/150 = 210
Tính phương sai:
- Phương sai = [(75-210)²×6 + (125-210)²×9 + (175-210)²×39 + (225-210)²×66 + (275-210)²×30]/150
- Phương sai = 2425
Độ lệch chuẩn = √2425 ≈ 49,24
Đáp án A: 49,24
Câu 5: Tập nghiệm của phương trình log0,2(x-2) > -2
Vì 0 < 0,2 < 1, nên hàm logarit cơ số 0,2 là hàm giảm.
Chuyển bất đẳng thức:
log0,2(x-2) > -2 ⟺ x-2 < (0,2)^(-2) = 25
⟺ x < 27
Đồng thời, để logarit có nghĩa: x-2 > 0 ⟺ x > 2
Vậy tập nghiệm là (2;27)
Đáp án A: (2;27)
Câu 8: Phương trình tham số đường thẳng d
Đường thẳng d qua điểm M(3;-1;4) và có vector chỉ phương u⃗ = (-2;4;5)
Phương trình tham số của d có dạng:
{
x = 3 – 2t
y = -1 + 4t
z = 4 + 5t
}
Đáp án C: {x = 3-2t, y = −1+4t, z = 4+5t}
Câu 9: Góc giữa đường thẳng SC và mặt phẳng (ABC)
Thiết lập hệ tọa độ với A tại gốc, B(a,0,0), C(a,a,0), S(0,0,a√2).
Vector SC⃗ = (a,a,-a√2)
Vector pháp tuyến của mặt phẳng ABC là (0,0,1)
Góc φ giữa SC⃗ và pháp tuyến:
cos(φ) = |SC⃗ · (0,0,1)| / (|SC⃗|·|(0,0,1)|)
= a√2 / (a√4) = 1/√2
φ = 45°
Góc giữa đường thẳng SC và mặt phẳng (ABC) = 90° – 45° = 45°
Đáp án C: 45°
Câu 11: Họ tất cả các nguyên hàm của hàm số f(x) = 5^x
Công thức nguyên hàm của a^x là a^x/ln(a) + C
Áp dụng: ∫5^x dx = 5^x/ln(5) + C
Đáp án A: 5^x/ln(5) + C
Câu 12: Phương trình mặt cầu có tâm I(-1;2;-3), bán kính R = 3
Phương trình mặt cầu có tâm (h,k,l) và bán kính R:
(x-h)² + (y-k)² + (z-l)² = R²
Thay số:
(x-(-1))² + (y-2)² + (z-(-3))² = 3²
(x+1)² + (y-2)² + (z+3)² = 9
Đáp án B: (x+1)² + (y-2)² + (z+3)² = 9
PHẦN II: Câu trắc nghiệm đúng sai
Câu 2: Về khảo sát tình trạng công việc
a) Xác suất chọn được một nam là 5/9
P(Nam) = (460+40)/900 = 500/900 = 5/9 ⟹ ĐÚNG
b) Xác suất chọn được một người có việc làm là 2/3
P(Có việc làm) = (460+140)/900 = 600/900 = 2/3 ⟹ ĐÚNG
c) Tỉ lệ nữ thất nghiệp cao gấp 7 lần nam
P(Thất nghiệp|Nam) = 40/500 = 0,08
P(Thất nghiệp|Nữ) = 260/400 = 0,65
0,65/0,08 = 8,125 ≠ 7 ⟹ SAI
d) Xác suất người có việc làm là nữ là 7/30
P(Nữ|Có việc làm) = 140/600 = 7/30 ⟹ ĐÚNG
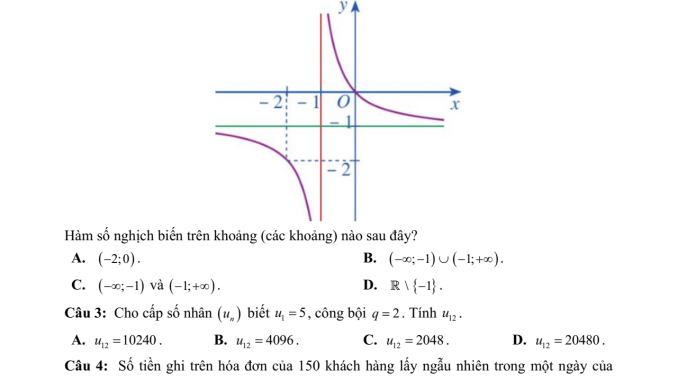
Câu 3: Hàm số f(x) = (x-2)/(x+1)
a) Đạo hàm f'(x) = 3/(x+1)²
Áp dụng quy tắc lượng tử: f'(x) = [(x+1) – (x-2)]/(x+1)² = 3/(x+1)² ⟹ ĐÚNG
b) Giá trị lớn nhất trên (-1;3] bằng 1
Khi x → -1⁺, f(x) → +∞
Vậy không có giá trị lớn nhất hữu hạn ⟹ SAI
c) Không thể xác định vì không có hình vẽ
d) f(0) = 2, f(-2) = 0
f(0) = (0-2)/(0+1) = -2 ≠ 2
f(-2) = (-2-2)/(-2+1) = -4/(-1) = 4 ≠ 0 ⟹ SAI
Câu 4: Lợi nhuận biên P'(x) = -0,0008x+10,4
a) Lợi nhuận khi bán 50 sản phẩm đầu tiên
P(50) – P(0) = ∫₀⁵⁰(-0,0008x+10,4)dx
= [-0,0004x² + 10,4x]₀⁵⁰
= (-0,0004×2500 + 10,4×50) – 0
= (-1 + 520) = 519 triệu đồng ⟹ ĐÚNG
b) Sự thay đổi lợi nhuận khi doanh số tăng từ 50 lên a đơn vị > 517 triệu đồng
P(a) – P(50) = ∫₅₀ᵃ(-0,0008x+10,4)dx
= [-0,0004x² + 10,4x]₅₀ᵃ
= (-0,0004a² + 10,4a) – (-0,0004×2500 + 10,4×50)
= -0,0004a² + 10,4a – 519 > 517
Giải bất phương trình: a ≥ 100 ⟹ ĐÚNG
c) P(x) = -0,0008x² + 10,4x
Tích phân P'(x): P(x) = -0,0004x² + 10,4x + C
Với P(0) = 0, ta có C = 0
Vậy P(x) = -0,0004x² + 10,4x ≠ -0,0008x² + 10,4x ⟹ SAI
d) Sự thay đổi lợi nhuận khi doanh số tăng từ 50 lên 55
P(55) – P(50) = ∫₅₀⁵⁵(-0,0008x+10,4)dx
= [-0,0004x² + 10,4x]₅₀⁵⁵
= (-0,0004×3025 + 10,4×55) – (-0,0004×2500 + 10,4×50)
= 51,79 triệu đồng ⟹ ĐÚNG
PHẦN III: Câu trắc nghiệm trả lời ngắn
Câu 2: Ước tính cân nặng của bé gái 5 tháng tuổi
Cho f'(t) = 0,00093t² – 0,04792t + 0,76806 (kg/tháng), f(0) = 3,3 kg
Cân nặng ở 5 tháng:
f(5) = f(0) + ∫₀⁵f'(t)dt
= 3,3 + ∫₀⁵(0,00093t² – 0,04792t + 0,76806)dt
= 3,3 + [0,00031t³ – 0,02396t² + 0,76806t]₀⁵
= 3,3 + (0,00031×125 – 0,02396×25 + 0,76806×5)
= 3,3 + (0,03875 – 0,599 + 3,8403)
= 3,3 + 3,28 = 6,58 kg
Câu 3: Nồng độ chất khử trùng không vượt quá p
Ban đầu có 150 lít nước, mỗi phút thêm 50 lít và 20g chất khử trùng.
Thể tích sau t phút: V(t) = 150 + 50t lít
Lượng chất khử trùng sau t phút: D(t) = 20t gram
Nồng độ f(t) = D(t)/V(t) = 20t/(150+50t) gram/lít
Giới hạn khi t → ∞: lim f(t) = lim 20t/(150+50t) = 20/50 = 0,4 gram/lít
Vậy p = 0,4
Câu 5: Xác suất trong bài toán lấy bi
Hộp I: 6 bi đỏ, 4 bi xanh
Hộp II: 5 bi đỏ, 5 bi xanh
Gọi:
- A₁: Minh lấy được bi đỏ từ hộp I
- A₂: Như lấy được bi đỏ từ hộp II
- B: Có bi đỏ được lấy ra
P(A₁) = 6/10 = 3/5
P(A₂) = 5/10 = 1/2
P(B) = P(A₁∪A₂) – P(A₁∩A₂)
= P(A₁) + P(A₂) – P(A₁)×P(A₂)
= 3/5 + 1/2 – 3/5×1/2
= 3/5 + 1/2 – 3/10
= 6/10 + 5/10 – 3/10
= 8/10 = 4/5
P(A₂|B) = P(A₂∩B)/P(B) = P(A₂)/P(B) = (1/2)/(4/5) = 5/8
Vậy a = 5, b = 8, và a-b = -3
Câu 6: Gia tốc lớn nhất của tàu Discovery
v(t) = 0,001302t³ – 0,09029t² + 23,61t – 3,083 (feet/s)
Gia tốc a(t) = v'(t) = 0,003906t² – 0,18058t + 23,61
Đạo hàm của gia tốc: a'(t) = 0,007812t – 0,18058
Điểm tới hạn: a'(t) = 0 ⟹ t ≈ 23,12 giây
Vì a”(t) = 0,007812 > 0, nên t = 23,12 là điểm cực tiểu.
Gia tốc đạt cực đại tại biên:
a(0) = 23,61
a(126) = 0,003906×126² – 0,18058×126 + 23,61 ≈ 62,9 feet/s²
Vậy gia tốc lớn nhất là 62,9 feet/s²
Đọc kỹ đề bài, đặc biệt là các điều kiện ràng buộc
Chú ý đến miền xác định của các hàm số
Kiểm tra các trường hợp đặc biệt (giá trị biên, điểm không liên tục…)
Với phần xác suất, cần xác định rõ không gian mẫu và các biến cố
- Đọc kỹ đề bài trước khi làm
- Phân bổ thời gian hợp lý cho từng câu
- Trình bày rõ ràng, sạch sẽ
- Kiểm tra kỹ đáp án trước khi nộp bài









