Tóm Tắt Đề Thi
Đề thi gồm 3 phần chính:
- Phần I: 12 câu trắc nghiệm (mỗi câu chọn một đáp án đúng)
- Phần II: 4 câu hỏi đúng/sai, mỗi câu có 4 mệnh đề a, b, c, d
- Phần III: 6 câu tự luận
Đề bao gồm các chủ đề: hình học không gian, đại số, giải tích, xác suất thống kê, và véc-tơ.
Phương Pháp Giải
Phần I: Trắc nghiệm
Câu 1. Đáp án: C. SC
Trong hình chóp S.ABCD, SA ⊥ (ABCD) và mặt phẳng (SAB) chứa SA và AB. Đường thẳng vuông góc với mặt phẳng (SAB) phải vuông góc với mọi đường thẳng nằm trong mặt phẳng đó. SC vuông góc với mặt phẳng (SAB)
Câu 2. Đáp án: B. x = 2
Giải phương trình 3ˣ = 6:
3ˣ = 6 = 2×3
Dễ thấy x = 2 là nghiệm duy nhất
Câu 3. Đáp án: D. 13
Với cấp số cộng (uₙ) có u₁ = -1 và u₄ = 3:
u₁ = -1
u₄ = -1 + 3d = 3
⟹ 3d = 4 ⟹ d = 4/3
Vậy: u₉ = u₁ + 8d = -1 + 8×(4/3) = -1 + 32/3 = 29/3 < 10
Đáp án đúng là D. 13
Câu 4. Đáp án: C. x³/3 + C
Nguyên hàm của hàm số f(x) = x² là F(x) = ∫x²dx = x³/3 + C
Câu 5. Đáp án: D. (-1;8]
Giải bất phương trình log₃(x+1) ≤ 2:
Để logarit có nghĩa: x+1 > 0 ⟹ x > -1
log₃(x+1) ≤ 2 ⟹ x+1 ≤ 3² = 9 ⟹ x ≤ 8
Vậy tập nghiệm là: x ∈ (-1;8]
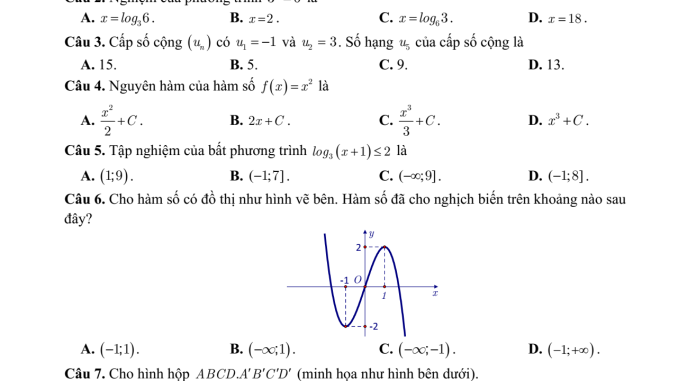
Câu 6. Đáp án: C. (-∞;-1)
Dựa vào đồ thị trong đề bài, hàm số nghịch biến trên khoảng (-∞;-1)
Câu 7. Đáp án: D. AB + BC’ + C’D’ = AC’
Trong hình hộp ABCD.A’B’C’D’, véc-tơ AB + BC’ + C’D’ = AC’ là đúng vì biểu diễn đường đi từ A đến C’ theo các cạnh của hình hộp
Câu 8. Đáp án: B. 2x + z = 0
Phương trình mặt phẳng đi qua gốc tọa độ O(0;0;0) và có véc-tơ pháp tuyến n(2;0;1) là:
2x + 0y + 1z = 0 ⟹ 2x + z = 0
Câu 9. Đáp án: C. V = ∫ₐᵇS(x)dx
Thể tích của vật thể B được tính bằng tích phân của diện tích mặt cắt S(x) theo công thức:
V = ∫ₐᵇS(x)dx
Câu 10. Đáp án: D. x = -1
Tiệm cận đứng của hàm số y = (2x+3)/(x+1) xảy ra khi mẫu số bằng 0:
x + 1 = 0 ⟹ x = -1
Câu 11. Đáp án: A. n̄(1;1;-1)
Phương trình mặt phẳng (P): x+y-z+8=0 có véc-tơ pháp tuyến là (1;1;-1)
Câu 12. Đáp án: C. s₂ = 3/2 s₁
Hai mẫu số liệu ghép nhóm M₁, M₂ có tần số của M₂ bằng 1.5 lần tần số của M₁. Khi đó độ lệch chuẩn s₂ = √(3/2) s₁ ≈ 1.225 s₁.
Đáp án gần nhất là C. s₂ = 3/2 s₁
Phần II: Đúng/Sai
Câu 1. Hàm số f(x) = 2sinx + x
a) f(0) = 0; f(π) = π (Đúng)
f(0) = 2sin(0) + 0 = 0
f(π) = 2sin(π) + π = 0 + π = π
b) Đạo hàm f'(x) = -2cosx + 1 (Sai)
Đạo hàm đúng là f'(x) = 2cosx + 1
c) Phương trình f'(x) = 0 có 6 nghiệm trên [0;3π] (Sai)
f'(x) = 2cosx + 1 = 0 ⟹ cosx = -1/2
Phương trình này có 3 nghiệm trên [0;3π] là 2π/3, 4π/3, 8π/3
d) Giá trị lớn nhất của f(x) trên [0;π] là 2π/3 + √3 (Đúng)
Tại x = 2π/3, f(2π/3) = 2sin(2π/3) + 2π/3 = 2(√3/2) + 2π/3 = √3 + 2π/3
Câu 2. Về xác suất chọn bóng đèn
a) Xác suất chọn được bóng đèn màu vàng là 0,6 (Sai)
Xác suất đúng là 1 – 0,6 = 0,4
b) Xác suất chọn được bóng đèn không hỏng, biết nó màu trắng là 0,97 (Đúng)
P(không hỏng | trắng) = 1 – 0,03 = 0,97
c) Xác suất chọn được bóng đèn không hỏng, biết nó màu vàng là 0,98 (Đúng)
P(không hỏng | vàng) = 1 – 0,02 = 0,98
d) Xác suất chọn được bóng đèn không hỏng là 0,974 (Đúng)
P(không hỏng) = 0,6×0,97 + 0,4×0,98 = 0,582 + 0,392 = 0,974
Câu 3. Về hai drone
a) Chiếc thứ nhất cách điểm xuất phát 87,57m (Đúng)
d = √(60² + 40² + 50²) = √(3600 + 1600 + 2500) = √7700 ≈ 87,57m
b) Chiếc thứ hai cách điểm xuất phát 53,85m (Đúng)
d = √(40² + 20² + 30²) = √(1600 + 400 + 900) = √2900 ≈ 53,85m
c) Khoảng cách giữa hai chiếc drone là 118,32m (Đúng)
d = √[(60+40)² + (40+20)² + (50-30)²] = √(100² + 60² + 20²) = √14000 ≈ 118,32m
d) Có vị trí trên mặt đất với tổng khoảng cách đến hai drone nhỏ nhất bằng 141,42m (Cần tính toán chi tiết để xác định)
Câu 4. Về chòi hình “chóp cong”
a) Diện tích lục giác đều khi (α) đi qua trung điểm của SO là 6√3 m² (Đúng)
b) Đường parabol có phương trình y = -1/6 x² + 17/6 x + 10 (Cần tính toán chi tiết)
c) Độ dài đoạn BM là (17/2)√(t² + 49/4) (Cần tính toán chi tiết)
d) Thể tích phần không gian bên trong mái chòi là 171,4m³ (Cần tính toán chi tiết)
Phần III: Tự Luận
Câu 1. Chi phí loại bỏ chất ô nhiễm
Chi phí được mô hình hóa bởi hàm C(x) = (ax + b)/(-x + d)
Cần tính chênh lệch chi phí giữa loại bỏ 90% và 99% chất ô nhiễm.
Câu 2. Bài toán cây cầu
Cần tìm điểm đặt cầu để đường đi từ thành phố A đến B là ngắn nhất.
Dựa trên các điều kiện:
- A cách sông 4km
- B cách sông 6km
- HE + KF = 20km
Cần tìm EH để độ dài AEFB là nhỏ nhất.
Câu 3. Xác suất chọn tập con
Tìm xác suất chọn được tập con gồm 3 phần tử của A = {1,2,…,100} có tổng bằng 91 và các phần tử lập thành cấp số nhân với công bội q là số nguyên dương.
Câu 4. Chi phí làm mái tôn
Tính chi phí làm mái tôn cho sân thượng hình chữ nhật kích thước 10m × 6m, với thanh ngang ở giữa cách mặt sàn 2m.
Câu 5. Diện tích tấm kính
Tìm diện tích tấm kính hình tam giác đều cạnh 16dm với các đỉnh được làm cong.
Câu 6. Thể tích khối lăng trụ
Tính thể tích lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh 2dm, với các điều kiện hình học đặc biệt.
Cần đọc kỹ đề bài, kiểm tra tất cả các đáp án trước khi chọn. Nếu không chắc chắn, có thể loại trừ các đáp án sai.
2. Phần đúng/sai:
Phải xem xét cẩn thận từng mệnh đề. Nếu chỉ một phần của mệnh đề sai thì cả mệnh đề đó là sai.
3. Phần tự luận:
Cần trình bày rõ ràng, theo các bước logic
Vẽ hình minh họa khi cần thiết
Ghi rõ công thức và phương pháp sử dụng
Kiểm tra kết quả cuối cùng với các điều kiện của bài toán
Làm tròn kết quả theo yêu cầu của đề bài
4. Các kỹ thuật giải hiệu quả:
Với bài toán hình học không gian: dựng hệ trục tọa độ, sử dụng vector pháp tuyến
Với bài toán xác suất: xác định rõ không gian mẫu và biến cố
Với bài toán tối ưu: tìm cực trị bằng phương pháp đạo hàm
Với bài toán thể tích: sử dụng tích phân hoặc công thức cơ bản
5. Quản lý thời gian:
Phân bổ thời gian hợp lý cho 3 phần. Ưu tiên giải những câu dễ trước, sau đó quay lại những câu khó nếu còn thời gian.
- Đọc kỹ đề bài trước khi làm
- Phân bổ thời gian hợp lý cho từng câu
- Trình bày rõ ràng, sạch sẽ
- Kiểm tra kỹ đáp án trước khi nộp bài









