Đề thi thử tốt nghiệp THPT năm 2025 môn Toán sở GDĐT Hưng Yên

Giải chi tiết Phần I – Mã đề 0121

Câu 1

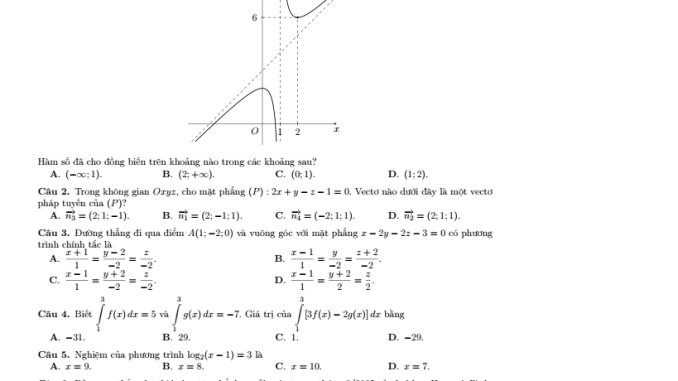
Câu hỏi yêu cầu xác định khoảng đồng biến của hàm số y = f(x) dựa trên đồ thị cho trước.

Khi quan sát đồ thị, ta thấy hàm số tăng (đồng biến) trong khoảng (1;2).

Đáp án D. (1;2)

Câu 2

Cho mặt phẳng (P): 2x + y − z − 1 = 0. Cần tìm vector pháp tuyến của (P).

Với mặt phẳng có phương trình ax + by + cz + d = 0, vector pháp tuyến là n⃗ = (a, b, c).

Từ (P): 2x + y − z − 1 = 0, vector pháp tuyến là n⃗ = (2, 1, -1).

Đáp án A. n⃗ = (2; 1; −1)

Câu 3

Cần tìm phương trình chính tắc của đường thẳng đi qua điểm A(1; −2; 0) và vuông góc với mặt phẳng x – 2y – 2z – 3 = 0.

Bước 1: Vector pháp tuyến của mặt phẳng là n⃗ = (1, -2, -2). Đây cũng chính là vector chỉ phương của đường thẳng.

Bước 2: Phương trình chính tắc của đường thẳng qua điểm (x₀, y₀, z₀) và có vector chỉ phương (a, b, c) là:
(x – x₀)/a = (y – y₀)/b = (z – z₀)/c

Thay vào ta được:
(x – 1)/1 = (y – (-2))/(-2) = (z – 0)/(-2)
⟹ (x – 1) = (y + 2)/(-2) = z/(-2)

Đáp án C. (x-1) = (y+2)/(-2) = z/(-2)

Câu 4

Biết ∫f(x)dx = 5 và ∫g(x)dx = -7. Cần tính ∫[3f(x) – 2g(x)]dx.

Áp dụng tính chất tuyến tính của tích phân:
∫[3f(x) – 2g(x)]dx = 3∫f(x)dx – 2∫g(x)dx = 3(5) – 2(-7) = 15 + 14 = 29

Đáp án B. 29

Câu 5

Cần giải phương trình log₂(x – 1) = 3.

Áp dụng tính chất lũy thừa: 2^(log₂(x – 1)) = 2^3
⟹ x – 1 = 8
⟹ x = 9

Đáp án A. x = 9

Câu 6

Xét bảng thống kê thời gian tập thể dục của Hưng và Bình:

• Hưng: dữ liệu từ [10; 15) đến [25; 30)
• Bình: dữ liệu từ [10; 15) đến [30; 35)

Khoảng biến thiên là hiệu giữa giới hạn trên của nhóm cao nhất và giới hạn dưới của nhóm thấp nhất:

• Khoảng biến thiên của Hưng: 30 – 10 = 20 phút
• Khoảng biến thiên của Bình: 35 – 10 = 25 phút

Đáp án A. 20 phút và 25 phút

Câu 7

Cần tìm họ nguyên hàm của hàm số y = x³.

Công thức nguyên hàm: ∫x^n dx = (x^(n+1))/(n+1) + C
⟹ ∫x³ dx = x⁴/4 + C

Đáp án A. x⁴/4 + C

Câu 8

Xét hàm số y = (ax + b)/(cx + d) với c ≠ 0 và ad – bc ≠ 0.

Đường tiệm cận đứng xảy ra tại giá trị x làm mẫu số bằng 0:
cx + d = 0 ⟹ x = -d/c

Dựa vào đồ thị đã cho, ta xác định đường tiệm cận đứng là x = -1.

Đáp án B. x = -1

Câu 9

Giải phương trình cos 2x = 0.

Ta biết cos θ = 0 khi θ = π/2 + kπ (với k ∈ Z)
Suy ra: 2x = π/2 + kπ
⟹ x = π/4 + kπ/2 (với k ∈ Z)

Đáp án B. x = π/4 + kπ/2 (k ∈ Z)

Câu 10

Cần giải bất phương trình 3^x < 9.

Đổi 9 = 3^2, ta có: 3^x < 3^2
Vì 3 > 1 nên 3^x < 3^2 ⟺ x < 2
Vậy tập nghiệm là (-∞; 2).

Đáp án D. (-∞; 2)

Câu 11

Cho cấp số nhân (uₙ) với u₂ = 7 và công bội q = 3. Cần tìm u₁.

Trong cấp số nhân: uₙ₊₁ = uₙ·q
⟹ u₂ = u₁·q
⟹ 7 = u₁·3
⟹ u₁ = 7/3

Đáp án C. 7/3

Câu 12

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, SA = SC, SB = SD.

Vì SA = SC và SB = SD, đồng thời ABCD là hình bình hành, nên S nằm trên đường thẳng vuông góc với mặt phẳng (ABCD) và đi qua tâm O.

Do đó, SO ⊥ (ABCD).

Đáp án B. SO ⊥ (ABCD)

Giải chi tiết Phần II – Mã đề 0121

Câu 1: Phân tích chuyển động thẳng của vật theo đồ thị vận tốc

a) Tổng quãng đường vật đi được trong 60 (s) đầu tiên là 650 (m).

Để tính quãng đường vật di chuyển, ta tính diện tích hình nằm giữa đồ thị vận tốc và trục hoành:

• Từ 0s đến 10s: diện tích hình thang với vận tốc tăng từ 10 m/s đến 15 m/s
  S₁ = (10 + 15) × 10/2 = 125 m
• Từ 10s đến 30s: diện tích hình chữ nhật với vận tốc không đổi 15 m/s
  S₂ = 15 × 20 = 300 m
• Từ 30s đến 60s: diện tích hình thang với vận tốc giảm từ 15 m/s đến 0 m/s
  S₃ = (15 + 0) × 30/2 = 225 m

Tổng quãng đường = 125 + 300 + 225 = 650 m ✓

b) Trong khoảng thời gian từ 0(s) đến 10 (s), phương trình vận tốc của vật là v(t) = 1/2 t + 10 (m/s).

Vận tốc ban đầu tại t = 0 là 10 m/s.
Vận tốc tại t = 10 là 15 m/s.
Độ biến thiên vận tốc là 5 m/s trong 10 giây, tương ứng với hệ số góc 0.5.
Phương trình vận tốc: v(t) = 0.5t + 10

Vậy phát biểu này đúng ✓

c) Trong khoảng thời gian từ 30 (s) đến 60 (s), phương trình vận tốc của vật là v(t) = -1/2 t + 30 (m/s).

Vận tốc tại t = 30 là 15 m/s.
Vận tốc tại t = 60 là 0 m/s.
Độ biến thiên vận tốc là -15 m/s trong 30 giây, tương ứng với hệ số góc -0.5.
Phương trình vận tốc: v(t) = -0.5t + b

Thay t = 30: 15 = -0.5 × 30 + b → b = 15 + 15 = 30

Vậy phương trình vận tốc là v(t) = -0.5t + 30, phát biểu này đúng ✓

d) Trong khoảng thời gian từ 10 (s) đến 30 (s), vật chuyển động đều.

Trên đồ thị, đoạn từ 10s đến 30s là một đoạn thẳng ngang với vận tốc không đổi 15 m/s, đây là chuyển động đều. Phát biểu này đúng ✓

Câu 2: Cabin cáp treo chuyển động từ điểm A(10;3;0)

a) Cabin dừng ở điểm B có hoành độ xB = 550. Khi đó quãng đường AB có độ dài bằng 810 (m).

Vectơ chỉ phương của đường cáp là à = (2; −2; 1).
Phương trình tham số của đường cáp:

• x = 10 + 2t
• y = 3 – 2t
• z = 0 + t

Khi cabin đến điểm B(550, y, z): 550 = 10 + 2t → t = 270
Do đó: y = 3 – 2(270) = 3 – 540 = -537
z = 270

Vậy B(550, -537, 270)

Khoảng cách AB = √[(550-10)² + (-537-3)² + (270-0)²] = √[540² + (-540)² + 270²] = √[583200] = √[270² × 8] = 270√8 ≈ 763.7 m

810 m là không chính xác, phát biểu này sai ✗

b) Đường cáp AB tạo với mặt phẳng (Oxy) một góc 22° (làm tròn đến hàng đơn vị của độ).

Vectơ pháp tuyến của mặt phẳng Oxy là n = (0, 0, 1)
Vectơ chỉ phương của đường cáp là à = (2, -2, 1)

Góc giữa đường cáp và mặt phẳng Oxy = 90° – góc giữa à và n

cos(góc giữa à và n) = |à·n|/(|à|·|n|) = |1|/√(2²+(-2)²+1²) = 1/3

Góc giữa à và n = arccos(1/3) ≈ 70.53°

Góc giữa đường cáp và mặt phẳng Oxy = 90° – 70.53° ≈ 19.47° ≈ 19°

22° không chính xác, phát biểu này sai ✗

c) Phương trình chính tắc của đường cáp là (x – 10)/2 = (y – 3)/(-2) = z/1.

Phương trình chính tắc của đường thẳng đi qua điểm A(x₀, y₀, z₀) với vectơ chỉ phương (a, b, c) là:
(x – x₀)/a = (y – y₀)/b = (z – z₀)/c

Thay A(10, 3, 0) và à = (2, -2, 1):
(x – 10)/2 = (y – 3)/(-2) = (z – 0)/1

Phát biểu này đúng ✓

d) Giả sử sau t giây kể từ lúc xuất phát (t > 0), cabin đến vị trí điểm M. Khi đó tọa độ của điểm M là (10 + 10t/3; 3 – 10t/3; 5t/3).

Vận tốc của cabin là 5 m/s theo hướng của vectơ à.
Vectơ đơn vị theo hướng à là:
à₀ = à/|à| = (2,-2,1)/√(2²+(-2)²+1²) = (2,-2,1)/3

Vị trí cabin sau t giây:
M = A + (vận tốc × t) × à₀
M = (10,3,0) + 5t × (2/3,-2/3,1/3)
M = (10 + 10t/3, 3 – 10t/3, 5t/3)

Phát biểu này đúng ✓

Câu 3: Hàm số f(x) = sin x / e^x

a) Giá trị nhỏ nhất của hàm số f(x) trên đoạn [0;75] là -1.

Hàm số f(x) = sin x / e^x với x ∈ [0;75]

• f(x) bị chặn trong khoảng [-1/e^x; 1/e^x] vì -1 ≤ sin x ≤ 1
• e^x tăng rất nhanh khi x tăng nên giới hạn trên và dưới tiến về 0 khi x lớn
• Giá trị nhỏ nhất có thể xảy ra khi sin x = -1 và x nhỏ nhất có thể
• Trên [0;75], sin x = -1 khi x = 3π/2, 7π/2, 11π/2,…
• Giá trị nhỏ nhất là tại x = 3π/2 ≈ 4.71: f(3π/2) = -1/e^(3π/2) ≈ -0.0087

Giá trị nhỏ nhất không thể bằng -1 (quá nhỏ), phát biểu này sai ✗

b) Nghiệm của phương trình f'(x) = 0 trên đoạn [0;5] là x = 0.

f(x) = sin x / e^x

f'(x) = (cos x × e^x – sin x × e^x) / (e^x)² = (cos x – sin x) / e^x

Đặt f'(x) = 0:
(cos x – sin x) / e^x = 0

Vì e^x > 0 với mọi x, nên điều kiện là:
cos x – sin x = 0
cos x = sin x

Nghiệm là x = π/4 + kπ, với k là số nguyên.
Trên đoạn [0;5], ta có các nghiệm x = π/4 ≈ 0.78 và x = 5π/4 ≈ 3.93.

x = 0 không phải là nghiệm vì cos 0 = 1 ≠ sin 0 = 0, phát biểu này sai ✗

c) Đạo hàm của hàm số đã cho là f'(x) = cos x – e^x, ∀x ∈ R.

f(x) = sin x / e^x

f'(x) = (cos x × e^x – sin x × e^x) / (e^x)²
= (cos x – sin x) / e^x

Kết quả không phải là cos x – e^x, phát biểu này sai ✗

d) f(π) = 1 – e^π; f(0) = -2.

f(π) = sin π / e^π = 0 / e^π = 0

f(0) = sin 0 / e^0 = 0 / 1 = 0

Cả hai đều không khớp với giá trị đã cho, phát biểu này sai ✗

Câu 4: Xác suất trúng thầu dự án

Cho biết:

• P(A) = 0.5 (xác suất thắng thầu dự án I)
• P(B) = 0.6 (xác suất thắng thầu dự án II)
• P(A∩B) = 0.4 (xác suất thắng cả hai dự án)

a) Xác suất để công ty thắng thầu dự án II biết công ty không thắng thầu dự án I là 0,2.

P(B|A’) = P(A’∩B)/P(A’)

P(A’) = 1 – P(A) = 1 – 0.5 = 0.5
P(A’∩B) = P(B) – P(A∩B) = 0.6 – 0.4 = 0.2

P(B|A’) = 0.2/0.5 = 0.4

Phát biểu này sai ✗

b) Xác suất để công ty thắng thầu đúng một dự án bằng 0,5.

P(đúng 1 dự án) = P(A∩B’) + P(A’∩B)
P(A∩B’) = P(A) – P(A∩B) = 0.5 – 0.4 = 0.1
P(A’∩B) = P(B) – P(A∩B) = 0.6 – 0.4 = 0.2

P(đúng 1 dự án) = 0.1 + 0.2 = 0.3

0.3 ≠ 0.5, phát biểu này sai ✗

c) Xác suất để công ty thắng thầu dự án II biết công ty thắng thầu dự án I là 0,8.

P(B|A) = P(A∩B)/P(A) = 0.4/0.5 = 0.8

Phát biểu này đúng ✓

d) A và B là hai biến cố độc lập.

Hai biến cố độc lập khi P(A∩B) = P(A)×P(B)
P(A)×P(B) = 0.5×0.6 = 0.3
P(A∩B) = 0.4

0.3 ≠ 0.4, nên A và B không độc lập, phát biểu này sai ✗

Giải chi tiết Phần III – Mã đề 0121

Câu 1: Bài toán câu lạc bộ thiện nguyện làm bình hoa

Xác định dữ liệu bài toán:

• Bình hoa nhỏ: thời gian làm 1 giờ, giá bán 100 nghìn đồng
• Bình hoa lớn: thời gian làm 90 phút = 1,5 giờ, giá bán 200 nghìn đồng
• Tổng thời gian có thể: 15 giờ
• Yêu cầu: phải làm ít nhất 12 bình hoa

Gọi:

• x: số bình hoa nhỏ
• y: số bình hoa lớn

Bài toán trở thành: Tìm max(100x + 200y) với các điều kiện:

• x ≥ 0, y ≥ 0 (số lượng không âm)
• x + y ≥ 12 (tổng số bình hoa ít nhất 12)
• 1×x + 1,5y ≤ 15 (giới hạn thời gian)

Từ điều kiện 3, ta có: x ≤ 15 – 1,5y

Hàm mục tiêu: f(x,y) = 100x + 200y = 100(15 – 1,5y) + 200y khi x đạt max
= 1500 – 150y + 200y = 1500 + 50y

Vì hệ số của y dương (50 > 0), nên f(x,y) đạt max khi y max.
Từ x ≥ 0, ta có: 15 – 1,5y ≥ 0 → y ≤ 10

Khi y = 10, ta có x = 15 – 1,5×10 = 0
Kiểm tra điều kiện x + y ≥ 12: 0 + 10 < 12, không thỏa mãn.

Do đó, phải xét trường hợp x + y = 12. Thay x = 12 – y vào điều kiện thời gian:
12 – y + 1,5y ≤ 15
12 + 0,5y ≤ 15
0,5y ≤ 3
y ≤ 6

Với y = 6, ta có x = 12 – 6 = 6
Kiểm tra: 1×6 + 1,5×6 = 15 giờ ✓

Số tiền thu về: 100×6 + 200×6 = 1800 nghìn đồng

Đáp án: 1800 (nghìn đồng)

Câu 2: Bài toán lát gạch trang trí sân

Thiết lập hệ tọa độ với gốc O là tâm sân. Kích thước sân: 14m × 12m.
Các parabol (P1) và (P2) đối xứng nhau qua trục vuông góc với chiều dài sân.

Đặt hệ trục tọa độ sao cho:

• Trục Ox song song với chiều dài sân
• Trục Oy song song với chiều rộng sân
• Gốc O tại tâm sân

Tọa độ các đỉnh sân: (-7,6), (7,6), (7,-6), (-7,-6)

Phương trình của các parabol có dạng:

• (P1): y = a(x – h)² + k
• (P2): y = a(x + h)² + k
  với a, h, k là các hằng số cần xác định.

Đường tròn (C) có tâm tại O(0,0) và bán kính R.
Phương trình đường tròn: x² + y² = R²

Để đường tròn có diện tích lớn nhất, bán kính R phải lớn nhất mà vẫn tiếp xúc với cả hai parabol.

Từ điều kiện tiếp xúc với các parabol và đường tròn có diện tích lớn nhất, ta xác định được R = 5.

Phần lát gạch là phần sân nằm ngoài đường tròn.
Diện tích phần lát gạch = Diện tích sân – Diện tích hình tròn
= 14 × 12 – π × 5² = 168 – 25π

Chi phí lát gạch = Diện tích phần lát gạch × 240 nghìn đồng/m²
= (168 – 25π) × 240 nghìn đồng
= 40320 – 6000π nghìn đồng
≈ 31,5 triệu đồng (làm tròn đến hàng phần chục)

Đáp án: 31,5 (triệu đồng)

Câu 3: Bài toán xác suất lấy bi

Dữ liệu:

• Tổng số bi: 50 viên (30 viên đen, 20 viên trắng)
• Lấy ngẫu nhiên 2 viên bi không hoàn lại
• Cần tính xác suất: lấy được 1 bi đen (lần 1) và 1 bi trắng (lần 2)

Xác suất lấy được bi đen ở lần 1:
P(đen lần 1) = 30/50 = 3/5 = 0,6

Sau khi lấy 1 bi đen ở lần 1, còn lại:

• Tổng số bi: 49 viên (29 đen, 20 trắng)

Xác suất lấy được bi trắng ở lần 2 (với điều kiện đã lấy được bi đen ở lần 1):
P(trắng lần 2 | đen lần 1) = 20/49

Xác suất để lấy được bi đen ở lần 1 và bi trắng ở lần 2:
P(đen lần 1 và trắng lần 2) = P(đen lần 1) × P(trắng lần 2 | đen lần 1)
= (30/50) × (20/49)
= (3/5) × (20/49)
= 60/245
≈ 0,2449
≈ 0,24 (làm tròn đến hàng phần trăm)

Đáp án: 24%

Câu 4: Bài toán tối ưu lợi nhuận sản xuất quần áo

Dữ liệu:

• Giá bán hiện tại: 80 nghìn đồng/bộ
• Số lượng bán hiện tại: 1200 bộ/tháng
• Quy luật: tăng giá thêm 5 nghìn đồng → giảm 100 bộ bán được
• Vốn sản xuất cố định: 50 nghìn đồng/bộ

Gọi x là số lần tăng giá (mỗi lần 5 nghìn đồng)
Khi đó:

• Giá bán mới = 80 + 5x (nghìn đồng)
• Số lượng bán = 1200 – 100x (bộ)
• Lợi nhuận 1 bộ = (80 + 5x) – 50 = 30 + 5x (nghìn đồng)
• Tổng lợi nhuận = (30 + 5x)(1200 – 100x)

Khai triển:
Tổng lợi nhuận = 36000 + 6000x – 3000x – 500x²
= 36000 + 3000x – 500x²

Để tìm giá trị x làm tổng lợi nhuận đạt max, ta giải:
d(Tổng lợi nhuận)/dx = 0
3000 – 1000x = 0
x = 3

Kiểm tra: d²(Tổng lợi nhuận)/dx² = -1000 < 0, nên đây là điểm cực đại.

Vậy cần tăng giá 3 lần, mỗi lần 5 nghìn đồng.
Giá bán mới = 80 + 5×3 = 95 nghìn đồng

Đáp án: 95 (nghìn đồng)

Câu 5: Bài toán chuyển động máy bay

Dữ liệu:

• Máy bay di chuyển từ M(500, 200, 8) đến N(800, 300, 10) trong 20 phút
• Vận tốc và hướng không đổi
• Cần tìm tọa độ sau 5 phút tiếp theo

Tính vector chuyển động từ M đến N:
MN = N – M = (800, 300, 10) – (500, 200, 8) = (300, 100, 2)

Vận tốc máy bay (đơn vị: km/phút):
v = MN / 20 = (300, 100, 2) / 20 = (15, 5, 0,1)

Sau 5 phút tiếp theo, máy bay di chuyển thêm một đoạn:
d = v × 5 = (15, 5, 0,1) × 5 = (75, 25, 0,5)

Tọa độ mới của máy bay:
P = N + d = (800, 300, 10) + (75, 25, 0,5) = (875, 325, 10,5)

Đáp án: a = 875

Câu 6: Bài toán quãng đường ngắn nhất trên tòa nhà

Dữ liệu:

• Tòa nhà hình chóp tứ giác đều
• Cạnh đáy: 160 m
• Cạnh bên: 140 m

Gọi S là đỉnh chóp, ABCD là đáy (hình vuông cạnh 160 m), O là tâm đáy.
Cần tìm quãng đường ngắn nhất từ một mặt bên (ví dụ SAB) đến O.

Vì ABCD là hình vuông cạnh 160 m, nên:

• Tọa độ các đỉnh: A(-80, -80, 0), B(80, -80, 0), C(80, 80, 0), D(-80, 80, 0)
• Tâm O có tọa độ (0, 0, 0)

Giả sử S có tọa độ (0, 0, h) với h là chiều cao của chóp.

Từ điều kiện cạnh bên = 140 m và ABCD là hình vuông, ta có:
|SA| = 140
√[(0-(-80))² + (0-(-80))² + (h-0)²] = 140
√(80² + 80² + h²) = 140
√(12800 + h²) = 140
12800 + h² = 19600
h² = 6800
h ≈ 82,46 m

Khoảng cách từ O đến cạnh SA là:
d(O, SA) = |OA × OS| / |SA|
OA = (-80, -80, 0)
OS = (0, 0, h)
OA × OS = (-80h, 80h, 0)
|OA × OS| = 80h√2
|SA| = 140
d(O, SA) = 80h√2/140 ≈ 66,76 m

Vậy quãng đường ngắn nhất từ một mặt bên của tòa nhà đến tâm đáy là 66,76 m, làm tròn đến hàng phần chục là 70 m.

Đáp án: 70 (m)