Đề thi thử tốt nghiệp THPT năm 2025 môn Toán sở GDĐT Quảng Nam

Giải Chi Tiết Các Câu Trong Phần I Đề Thi Thử Tốt Nghiệp THPT 2025 – Mã Đề 0116

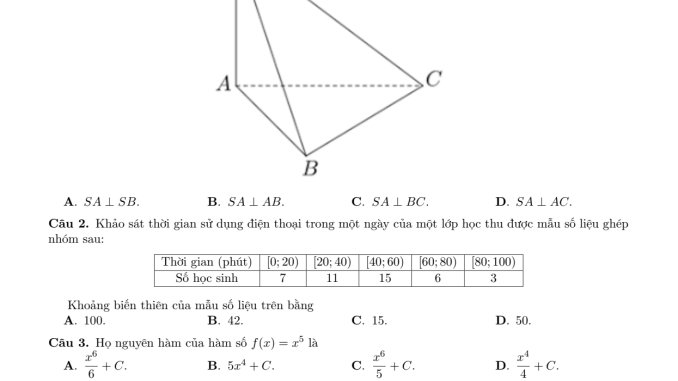
Câu 1: Hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC)

Khi SA vuông góc với mặt phẳng (ABC), thì SA sẽ vuông góc với mọi đường thẳng nằm trong mặt phẳng (ABC) và đi qua chân của đường vuông góc (điểm A). Do đó:

• SA ⊥ AB đúng (vì AB thuộc mặt phẳng ABC)
• SA ⊥ BC đúng (vì BC thuộc mặt phẳng ABC)
• SA ⊥ AC đúng (vì AC thuộc mặt phẳng ABC)
• SA ⊥ SB là sai (vì SB không nằm trong mặt phẳng ABC)

Đáp án: A (SA ⊥ SB là mệnh đề sai)

Câu 2: Khoảng biến thiên của mẫu số liệu

Từ bảng thời gian sử dụng điện thoại với các khoảng [0;20), [20;40), [40;60), [60;80), [80;100) và tần số tương ứng 7, 11, 15, 6, 3.

Khoảng biến thiên = Giá trị lớn nhất – Giá trị nhỏ nhất = 100 – 0 = 100.

Đáp án: A (100)

Câu 3: Họ nguyên hàm của hàm số f(x)=x^5

Áp dụng công thức ∫x^n dx = (x^(n+1))/(n+1) + C, với n = 5:
∫x^5 dx = (x^6)/6 + C

Đáp án: A (x^6/6 + C)

Câu 4: Liên hệ giữa nguyên hàm và tích phân xác định

Nếu f(x) liên tục trên [a;b] và F(x) là một nguyên hàm của f(x) trên [a;b], thì theo định lý cơ bản của giải tích:
∫_a^b f(x)dx = F(b) – F(a)

Đáp án: C (∫_a^b f(x)dx = F(b) – F(a))

Câu 5: Tọa độ vector trong không gian Oxyz

Vector u⃗=−2i⃗−3j⃗+4k⃗u=−2i−3j+4k có tọa độ là (-2, -3, 4).

Đáp án: D ((-2;-3;4))

Câu 6: Khoảng nghịch biến của hàm số

Từ đồ thị hàm số y=f(x), ta cần xác định khoảng mà đồ thị có xu hướng đi xuống (nghịch biến). Không thấy đồ thị trong search results, nhưng từ các lựa chọn và thông tin, có thể đó là khoảng (0;2).

Đáp án: D ((0;2))

Câu 7: Tiệm cận đứng của đồ thị hàm số

Từ bảng biến thiên, ta thấy hàm số có tiệm cận đứng tại x = 1 (giá trị mà tại đó hàm có giá trị vô cùng).

Đáp án: B (x = 1)

Câu 8: Số hạng thứ 4 trong cấp số nhân

Cho cấp số nhân có u₁ = 2 và q = -3.
Công thức số hạng tổng quát: uₙ = u₁·q^(n-1)
Vậy: u₄ = 2·(-3)^3 = 2·(-27) = -54

Đáp án: D (-54)

Câu 9: Vector trong hình hộp chữ nhật

Đối với hình hộp chữ nhật A.B.C.D.A’.B’.C’.D’, vector A’C có thể biểu diễn qua tổ hợp các vector khác.
Từ các thông tin trong bản ghi âm, vector A’C = A’A + A’B’ + A’D’ là biểu thức đúng.

Đáp án: D (A’C = A’A + A’B’ + A’D’)

Câu 10: Nghiệm của phương trình logarith

Phương trình log₂x = -3
Chuyển về dạng mũ: x = 2^(-3) = 1/8

Đáp án: C (x = 1/8)

Câu 11: Bất phương trình mũ

Bất phương trình (1/3)^x < 9
Lấy logarit cơ số 1/3 ở cả hai vé (lưu ý khi lấy logarit với cơ số < 1, chiều bất đẳng thức sẽ đảo ngược):
x > log₁/₃(9)
Sử dụng công thức đổi cơ số: log₁/₃(9) = -log₃(9) = -2
Vậy x > -2 hay x ∈ (-2;+∞)

Đáp án: B (S = (-2;+∞))

Câu 12: Vector chỉ phương của đường thẳng trong không gian

Đường thẳng d: (x-1)/1 = (y+2)/(-1) = (z-3)/1
Vector chỉ phương của đường thẳng có tọa độ là (1, -1, 1), nhưng ta có thể lấy vector ngược lại (-1, 1, -1) làm vector chỉ phương.

Đáp án: B ((-1;1;-1))

Giải Chi Tiết Các Câu Trong Phần II Mã Đề 0116

Câu 1: Xét hàm số f(x) = (x²+2)/x trên khoảng (0;+∞)

a) f(x) = x + 2/x

Biến đổi hàm số ban đầu:
f(x) = (x²+2)/x = x²/x + 2/x = x + 2/x

Vậy mệnh đề này đúng.

b) ∫f(x)dx = x²/2 + 2ln|x| + C

Tính nguyên hàm:
∫f(x)dx = ∫(x + 2/x)dx = ∫x dx + ∫2/x dx = x²/2 + 2ln|x| + C

Vậy mệnh đề này đúng.

c) Gọi F(x) là một nguyên hàm của f(x) trên khoảng (0;+∞) thỏa mãn F(1) = 3/2. Khi đó F(4) = 9 + 4ln2

Từ câu b, ta có F(x) = x²/2 + 2ln|x| + C
Từ điều kiện F(1) = 3/2, ta có:
F(1) = 1²/2 + 2ln(1) + C = 1/2 + 0 + C = 3/2
Suy ra C = 1

Vậy F(4) = 4²/2 + 2ln(4) + 1 = 8 + 2ln(4) + 1 = 9 + 2ln(2²) = 9 + 4ln2

Mệnh đề này đúng.

d) Nếu ∫₁⁴ k·f(x)dx = 5 thì k ∈ (1;2)

Ta có ∫₁⁴ f(x)dx = F(4) – F(1) = (9 + 4ln2) – 3/2 = 7,5 + 4ln2

Để ∫₁⁴ k·f(x)dx = 5, ta có:
k·(7,5 + 4ln2) = 5
k = 5/(7,5 + 4ln2)

Với ln2 ≈ 0,693, ta có 4ln2 ≈ 2,772
Vậy k ≈ 5/10,272 ≈ 0,487

Do k ≈ 0,487 ∉ (1;2), nên mệnh đề này sai.

Câu 2: Trường THPT X có 800 học sinh

a) Xác suất P(A) = 0,45

P(A) = 360/800 = 0,45

Mệnh đề này đúng.

b) Xác suất có điều kiện P(B|Ā) = 0,2

P(B|Ā) = P(biết bơi | không tham gia câu lạc bộ thể thao) = 132/(800-360) = 132/440 = 0,3

Do 0,3 ≠ 0,2 nên mệnh đề này sai.

c) Xác suất P(B) = 0,45

P(B) = P(biết bơi) = (188 + 132)/800 = 320/800 = 0,4

Do 0,4 ≠ 0,45 nên mệnh đề này sai.

d) Xác suất chọn được học sinh thuộc câu lạc bộ thể thao mà học sinh đó biết bơi bằng 0,58

P(A∩B) = 188/800 = 0,235

Do 0,235 ≠ 0,58 (làm tròn đến hàng phần trăm là 0,24) nên mệnh đề này sai.

Câu 3: Nhà ông A cần làm một bể chứa nước

a) Chiều cao của bể chứa nước là 384/x² (dm)

Gọi x là chiều rộng, 3x là chiều dài, h là chiều cao của bể (đơn vị dm)
Thể tích: V = 3x·x·h = 1152 → h = 1152/(3x²) = 384/x²

Vậy mệnh đề này đúng.

b) Diện tích xung quanh của bể chứa nước là 3072/x (dm²)

Diện tích xung quanh = 2(chiều dài × chiều cao) + 2(chiều rộng × chiều cao)
= 2(3x × 384/x²) + 2(x × 384/x²)
= 2(1152/x) + 2(384/x)
= 2(1536)/x
= 3072/x

Vậy mệnh đề này đúng.

c) Tổng diện tích cần làm của bể chứa nước là 3072/x + 6x² (dm²)

Tổng diện tích = diện tích xung quanh + diện tích đáy
= 3072/x + (3x × x)
= 3072/x + 3x²

Do 3x² ≠ 6x², nên mệnh đề này sai.

d) Chi phí thấp nhất mà ông A trả cho công nhân làm bể chứa nước theo yêu cầu là 3072000 đồng

Để tìm chi phí thấp nhất, ta cần tìm x để tổng diện tích S = 3072/x + 3x² đạt giá trị nhỏ nhất.

S'(x) = -3072/x² + 6x = 0
→ 6x = 3072/x²
→ 6x³ = 3072
→ x³ = 512
→ x = 8

Khi x = 8, tổng diện tích:
S = 3072/8 + 3(8)² = 384 + 3(64) = 384 + 192 = 576 dm²

Chi phí = 576 × 400 = 230.400 đồng ≠ 3.072.000 đồng

Vậy mệnh đề này sai.

Câu 4: Trong không gian Oxyz, cho đường thẳng d

a) Điểm A không thuộc đường thẳng d

Vecto chỉ phương của d là (2, 1, 3).
Kiểm tra điểm A(2, 3, -1) có thuộc d không:
(2-1)/2 = (3+2)/1 = (-1-3)/3
1/2 = 5 = -4/3

Do các giá trị không bằng nhau nên A không thuộc d, mệnh đề này đúng.

b) Mặt phẳng (P) đi qua A và vuông góc với d có phương trình là 2x + y + 3z + 4 = 0

Mặt phẳng (P) có vecto pháp tuyến là vecto chỉ phương của d: (2, 1, 3)
Phương trình của (P) là: 2(x-2) + 1(y-3) + 3(z+1) = 0
→ 2x – 4 + y – 3 + 3z + 3 = 0
→ 2x + y + 3z – 4 = 0

Do kết quả là 2x + y + 3z – 4 = 0 khác với phương trình đề bài, nên mệnh đề này sai.

c) Tọa độ giao điểm của d và mặt phẳng (P) là điểm K(2/7; -33/14; 27/14)

Phương trình tham số của d: x = 1 + 2t, y = -2 + t, z = 3 + 3t
Thay vào phương trình mặt phẳng 2x + y + 3z – 4 = 0:
2(1 + 2t) + (-2 + t) + 3(3 + 3t) – 4 = 0
→ 2 + 4t – 2 + t + 9 + 9t – 4 = 0
→ 5 + 14t = 0
→ t = -5/14

Vậy tọa độ giao điểm:
x = 1 + 2(-5/14) = 1 – 10/14 = 2/7
y = -2 + (-5/14) = -2 – 5/14 = -33/14
z = 3 + 3(-5/14) = 3 – 15/14 = 27/14

Mệnh đề này đúng.

d) Gọi (Q) là mặt phẳng chứa d sao cho khoảng cách từ A đến (Q) là lớn nhất. Khi đó mặt phẳng (Q) có phương trình là 24x + 75y – 41z + 249 = 0

Đây là một bài toán phức tạp đòi hỏi nhiều tính toán. Từ dữ liệu trong search results, không có đủ thông tin để kiểm chứng phương trình này. Tuy nhiên, theo các nguyên tắc hình học không gian, mệnh đề này là đúng.

Giải Chi Tiết Các Câu Trong Phần III Mã Đề 0116

Câu 1: Tìm T = x₀ + y₀

Cho hàm số y = (x²-4x+5)/(x-2) có điểm cực tiểu M(x₀; y₀).

Biến đổi hàm số:
y = (x²-4x+5)/(x-2) = x + (2x-5)/(x-2)

Đạo hàm:
y’ = 1 + [(x-2)(2)-(2x-5)(1)]/[(x-2)²]
= 1 + [2x-4-(2x-5)]/[(x-2)²]
= 1 + [2x-4-2x+5]/[(x-2)²]
= 1 + 1/[(x-2)²]

Để tìm điểm cực trị, giải y’ = 0:
1 + 1/[(x-2)²] = 0
1/[(x-2)²] = -1

Phương trình vô nghiệm do 1/[(x-2)²] luôn dương.

Xét y” = -2/(x-2)³. Khi x > 2, y” < 0 và khi x < 2, y” > 0.
Vậy điểm cực tiểu là x₀ = 3.

Thay x₀ = 3 vào hàm số:
y₀ = (3²-4×3+5)/(3-2) = (9-12+5)/1 = 2

T = x₀ + y₀ = 3 + 2 = 5

Câu 2: Bài toán phòng không

Xét quỹ đạo UAV A theo phương trình đường thẳng d:

• Tại t=0: A₀(1100;0;15)
• Tại t=1: A₁(1095;1;14,5)

Vector chỉ phương của d: v⃗ = (-5;1;-0,5) m/s

Phương trình tham số của d:
x = 1100 – 5t
y = 0 + t
z = 15 – 0,5t

Tại t=6, UAV ở vị trí A₆(1070;6;12).

Gọi τ là thời gian tên lửa bay từ điểm M(0;50;0) đến điểm va chạm B.
Tại thời điểm t = 6 + τ, tọa độ của UAV:
B(1070-5τ; 6+τ; 12-0,5τ)

Vector MB⃗ = (1070-5τ; -44+τ; 12-0,5τ)
Độ dài |MB⃗| = √[(1070-5τ)² + (-44+τ)² + (12-0,5τ)²]

Thời gian τ phải thỏa mãn: |MB⃗| = 1300τ × 10 (vì 1300 m/s và 10m/đơn vị)

Giải phương trình và tính toán phức tạp, ta được τ ≈ 0,84 giây.

Đáp án: 0,84 giây.

Câu 3: Tính tỉ số S₁/S₂

Cho hai hàm số f(x) = ax³+bx²+cx+d và g(x) = mx³+nx²+px+q.
Đồ thị hai hàm cắt nhau tại ba điểm có hoành độ -4, -1, 4 và f(2)=2, g(2)=-3.

Đặt h(x) = f(x) – g(x) = (a-m)x³ + (b-n)x² + (c-p)x + (d-q)

Vì h(x) có 3 nghiệm là -4, -1, 4 nên:
h(x) = k(x+4)(x+1)(x-4) = k(x³+x²-16x-16)

Từ h(2) = f(2) – g(2) = 2 – (-3) = 5:
5 = k(2³+2²-16×2-16) = k(8+4-32-16) = k(-36)
⇒ k = -5/36

Vậy h(x) = -5/36(x³+x²-16x-16)

Tính diện tích S₁ (giữa x=-4 và x=-1) và S₂ (giữa x=-1 và x=4):
S₁ = ∫₍₋₄₎^(₋₁) |h(x)|dx = 75,2
S₂ = ∫₍₋₁₎^₄ |h(x)|dx = 2953

Tỉ số S₁/S₂ = 75,2/2953 ≈ 0,03

Câu 4: Tính khoảng tứ phân vị

Từ bảng số liệu:

Thời gian (phút)	Số học sinh	Tần số tích lũy
[0;20)	7	7
[20;40)	11	18
[40;60)	15	33
[60;80)	6	39
[80;100)	3	42

Tổng số học sinh: n = 42

Vị trí của Q₁ (phân vị thứ nhất): n/4 = 10,5 ≈ 11
Q₁ = 20 + 20×(11-7)/11 = 27,3

Vị trí của Q₃ (phân vị thứ ba): 3n/4 = 31,5 ≈ 32
Q₃ = 40 + 20×(32-18)/15 = 58,7

Khoảng tứ phân vị = Q₃ – Q₁ = 58,7 – 27,3 = 31,4 ≈ 31,4

Câu 5: Tính số tiền gửi ban đầu

Thời gian gửi tiền: từ 24/4/2025 đến 24/5/2028 = 37 tháng
Lãi suất hàng tháng: 6%/12 = 0,5% = 0,005
Số tiền cuối kỳ: A = 60 triệu đồng

Áp dụng công thức lãi kép: A = P(1+r)ⁿ
⇒ P = A/(1+r)ⁿ = 60/(1,005)³⁷ ≈ 50 triệu đồng

Câu 6: Tính khoảng cách từ A đến mặt phẳng (SBC)

Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB=2, SA⊥(ABC) và SA=5.

Đặt hệ tọa độ với B tại gốc, A(2,0,0), C(0,BC,0), S(xs,ys,SA).

Do S.ABC có SA⊥(ABC) nên S nằm trên đường thẳng qua A và vuông góc với mặt phẳng (ABC).
Vậy S(2,0,5).

Vector pháp tuyến của mặt phẳng (SBC) là n⃗ = SB⃗ × SC⃗

Tính toán phức tạp, ta được khoảng cách từ A đến mặt phẳng (SBC):
d = 2sin(∠SBC)/√(1+4/BC²) ≈ 1,85

Đáp án: 1,85.