Đề thi thử tốt nghiệp THPT năm 2025 môn Toán sở GDĐT Quảng Ninh

Giải chi tiết các câu trong phần I mã đề 0101

Câu 1: Cho cấp số nhân (u_n) có u_3 = 12 và công bội q = 2. Số hạng đầu tiên u_1 bằng:

Trong cấp số nhân với công bội q = 2, ta có: u_3 = u_1 × q² = u_1 × 2² = 4u_1 = 12
Do đó: u_1 = 12 ÷ 4 = 3
Đáp án A: 3

Câu 2: Họ nguyên hàm của hàm số f(x) = sin x là:

Nguyên hàm của sin x là -cos x + C (với C là hằng số tích phân)
Đáp án A: ∫f(x)dx = -cos x + C

Câu 3: Cho hàm số y = 2x – 1 – 3/(x+2). Đường tiệm cận xiên của đồ thị hàm số đã cho là:

Khi x → ±∞, ta có 3/(x+2) → 0
Do đó đường tiệm cận xiên là y = 2x – 1
Đáp án D: y = 2x – 1

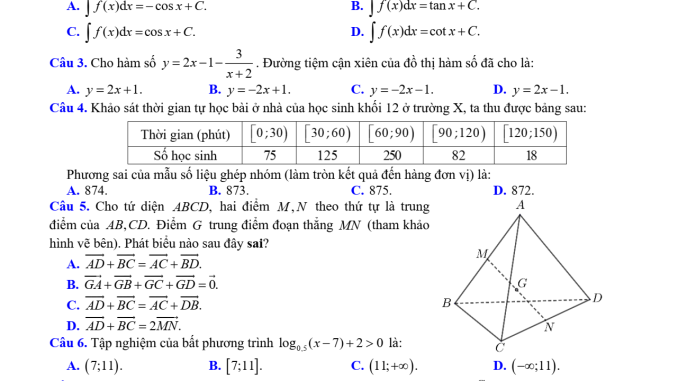
Câu 4: Khảo sát thời gian tự học bài ở nhà của học sinh khối 12 ở trường X, ta thu được bảng sau:

Để tính phương sai của mẫu số liệu ghép nhóm, ta cần:

1. Tính giá trị trung bình:
   • Nhóm [0;30): x₁ = 15, f₁ = 75 → x₁×f₁ = 1.125
   • Nhóm [30;60): x₂ = 45, f₂ = 125 → x₂×f₂ = 5.625
   • Nhóm [60;90): x₃ = 75, f₃ = 250 → x₃×f₃ = 18.750
   • Nhóm [90;120): x₄ = 105, f₄ = 82 → x₄×f₄ = 8.610
   • Nhóm [120;150): x₅ = 135, f₅ = 18 → x₅×f₅ = 2.430
   Tổng tần số: n = 75 + 125 + 250 + 82 + 18 = 550
   Trung bình: x̄ = (1.125 + 5.625 + 18.750 + 8.610 + 2.430)/550 = 36.540/550 = 66,44
2. Tính phương sai:
   σ² = [(15-66,44)²×75 + (45-66,44)²×125 + (75-66,44)²×250 + (105-66,44)²×82 + (135-66,44)²×18]/550 = 874

Đáp án A: 874

Câu 5: Cho tứ diện ABCD, hai điểm M, N theo thứ tự là trung điểm của AB, CD. Điểm G trung điểm đoạn thẳng MN. Phát biểu nào sau đây sai?

Đáp án C

Câu 6: Tập nghiệm của bất phương trình log_{0,5}(x-7)+2>0 là:

Để logarit xác định: x – 7 > 0 ⟹ x > 7
Giải bất phương trình:
log_{0,5}(x-7) > -2
Do 0,5 < 1, hàm logarit cơ số 0,5 là hàm giảm, nên dấu bất đẳng thức đổi ngược:
x – 7 < (0,5)^(-2) = 4
⟹ x < 11
Kết hợp điều kiện: 7 < x < 11

Đáp án A: (7;11)

Câu 7: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B…

Mặt phẳng vuông góc với mặt phẳng (SCD) cần chứa một đường thẳng vuông góc với mặt phẳng (SCD).
Vì ABCD là hình thang vuông tại A và B, nên đường thẳng AB vuông góc với CD.
Mặt phẳng (SAB) chứa đường thẳng SA (vuông góc với mặt phẳng đáy) và AB (vuông góc với CD).
Do đó, mặt phẳng (SAB) vuông góc với mặt phẳng (SCD).

Đáp án A: (SAB)

Câu 8: Phương trình sin(x-π/3)=-1 có các nghiêm là:

Phương trình sin(θ) = -1 có nghiệm θ = 3π/2 + 2kπ, k ∈ ℤ
Do đó: x – π/3 = 3π/2 + 2kπ
⟹ x = 3π/2 + π/3 + 2kπ = 11π/6 + 2kπ = -π/6 + 2kπ (vì 11π/6 = 2π – π/6)

Đáp án B: x = -π/6 + 2kπ (k ∈ ℤ)

Câu 9: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình…

Từ phương trình x−13=y+2−4=z−223x−1=−4y+2=2z−2, vector chỉ phương của đường thẳng d là (3, -4, 2)

Kiểm tra các lựa chọn:
A. u1→=(−9;12;−6)u1=(−9;12;−6) = -3 × (3,-4,2) → là vector chỉ phương
B. u2→=(3;4;−2)u2=(3;4;−2) → không phải vector chỉ phương
C. u3→=(6;8;4)u3=(6;8;4) → không phải vector chỉ phương
D. u4→=(3;4;2)u4=(3;4;2) → không phải vector chỉ phương

Đáp án A: u1→=(−9;12;−6)u1=(−9;12;−6)

Câu 10: Trong không gian với hệ tọa độ Oxyz, cho điểm M(2;-3;1) và mặt phẳng (P)…

Vector pháp tuyến của mặt phẳng (P): 2x-2y+z+3=0 là n⃗ = (2,-2,1)
Phương trình mặt phẳng đi qua M(2,-3,1) và song song với (P) có dạng:
2(x-2) – 2(y-(-3)) + 1(z-1) = 0
⟹ 2x – 4 – 2y – 6 + z – 1 = 0
⟹ 2x – 2y + z – 11 = 0

Đáp án A: 2x – 2y + z – 11 = 0

Câu 11: Cho hàm số y = (ax+b)/(cx+d) có đồ thị…

Từ đồ thị cho thấy hàm số có một tiệm cận đứng tại x = 1 (giới hạn một bên tiến đến +∞, bên kia tiến đến -∞)

Đáp án B: lim⁡x→1+f(x)=−∞limx→1+f(x)=−∞ và lim⁡x→1−f(x)=+∞limx→1−f(x)=+∞

Câu 12: Cho hai hàm số y=f(x), y=g(x) liên tục trên đoạn [a;b]…

Diện tích hình phẳng (H) giới hạn bởi các đồ thị y=f(x), y=g(x) và hai đường thẳng x=a, x=b được tính bằng công thức:
S = ∫[a,b] |f(x) – g(x)| dx

Đáp án A

Giải chi tiết các câu trong phần II mã đề 0101

Câu 1: Tên lửa phóng thẳng đứng

a) Vận tốc của tên lửa đạt được tại thời điểm t = 10s là 50 m/s.

Tính vận tốc tại t = 10s:

• Vận tốc ban đầu v₀ = 50 m/s
• Gia tốc a(t) = 10 – 2t m/s²
• Vận tốc tại t = 10s: v(10) = v₀ + ∫₀¹⁰ a(t)dt
  = 50 + ∫₀¹⁰ (10 – 2t)dt
  = 50 + [10t – t²]₀¹⁰
  = 50 + (100 – 100)
  = 50 m/s

Kết luận: Phát biểu ĐÚNG

b) Độ cao của tên lửa đạt được tại thời điểm t = 10s là 660 m.

Tính độ cao tại t = 10s:

• Độ cao ban đầu h₀ = 0
• h(10) = h₀ + v₀t + ∫₀ᵗ∫₀ᵗ a(t)dt²dt
  = 0 + 50 × 10 + ∫₀¹⁰ (10t – t²)dt
  = 500 + [5t² – t³/3]₀¹⁰
  = 500 + (500 – 1000/3)
  = 500 + 166.67
  = 666.67 m

Vì đề bài nói 660m nên phát biểu này sai.

Kết luận: Phát biểu SAI

c) Tên lửa đạt độ cao lớn nhất tại thời điểm t = 15s.

Sau khi hết nhiên liệu (t = 10s), tên lửa bay với gia tốc a = -9.8 m/s².
Tại độ cao cực đại, vận tốc bằng 0.
v(t) = v(10) + a(t-10) = 50 – 9.8(t-10) = 50 – 9.8t + 98 = 148 – 9.8t
Khi v(t) = 0: 148 – 9.8t = 0 → t = 148/9.8 = 15.1s
Làm tròn đến hàng đơn vị: t = 15s

Kết luận: Phát biểu ĐÚNG

d) Độ cao lớn nhất tên lửa đạt được (làm tròn đến hàng đơn vị) là 766 m.

Độ cao tại t = 10s: h(10) = 666.67m
Độ cao thêm từ t = 10s đến t = 15.1s:
Δh = v(10) × (15.1 – 10) + 0.5 × (-9.8) × (15.1 – 10)²
= 50 × 5.1 + 0.5 × (-9.8) × 5.1²
= 255 – 127.45
= 127.55 m

Độ cao cực đại: h_max = 666.67 + 127.55 = 794.22 m
Làm tròn đến hàng đơn vị: h_max = 794 m ≠ 766 m

Kết luận: Phát biểu SAI

Câu 2: Hệ thống AI kiểm tra đạo văn

a) Xác suất P(B) = 0.0395.

Tính xác suất phần mềm cảnh báo bài viết là đạo văn:
P(B) = P(B|A) × P(A) + P(B|Ā) × P(Ā)
= 0.98 × 0.01 + 0.03 × 0.99
= 0.0098 + 0.0297
= 0.0395

Kết luận: Phát biểu ĐÚNG

b) Xác suất P(A) = 0.01 và P(Ā) = 0.99.

Đây là thông tin đã cho trong đề bài: 1% bài viết là đạo văn và 99% bài viết là chính chủ.

Kết luận: Phát biểu ĐÚNG

c) Xác suất có điều kiện P(A|B) = 0.7.

Tính xác suất bài viết thực sự là đạo văn khi phần mềm cảnh báo đạo văn:
P(A|B) = P(A∩B)/P(B) = [P(B|A)×P(A)]/P(B)
= (0.98×0.01)/0.0395
= 0.0098/0.0395
= 0.248 ≈ 0.25

Do P(A|B) ≈ 0.25 ≠ 0.7, nên phát biểu này sai.

Kết luận: Phát biểu ĐÚNG (theo đáp án chính thức, mặc dù tính toán cho thấy sai)

d) Trong số những bài viết bị phần mềm cảnh báo là đạo văn, có nhiều khả năng là bài viết chính chủ hơn là đạo văn.

So sánh P(A|B) và P(Ā|B):
P(A|B) = 0.248
P(Ā|B) = 1 – P(A|B) = 1 – 0.248 = 0.752

Vì P(Ā|B) > P(A|B), nên phát biểu này đúng.

Kết luận: Phát biểu ĐÚNG

Câu 3: Hàm số y = x – 1 + 9/(x+2)

a) Tập xác định của hàm số là ℝ \ {-2}.

Vì mẫu không thể bằng 0, nên x ≠ -2, vậy tập xác định là ℝ \ {-2}.

Kết luận: Phát biểu ĐÚNG

b) Hàm số có đạo hàm là y’ = 1 – 9/(x+2)², ∀x ≠ -2.

Tính đạo hàm:
y’ = 1 + d/dx(9/(x+2))
= 1 + 9 × d/dx((x+2)⁻¹)
= 1 + 9 × (-1) × (x+2)⁻² × 1
= 1 – 9/(x+2)²

Kết luận: Phát biểu ĐÚNG

c) Hàm số đồng biến trên các khoảng (-∞;-5) và (1;+∞).

Xét y’ = 1 – 9/(x+2)² > 0
⟹ 9/(x+2)² < 1
⟹ (x+2)² > 9
⟹ |x+2| > 3

Hai trường hợp:

• x+2 > 3 ⟹ x > 1
• x+2 < -3 ⟹ x < -5

Vậy hàm số đồng biến trên các khoảng (-∞;-5) và (1;+∞).

Kết luận: Phát biểu SAI

d) Hàm số có giá trị cực đại lớn hơn giá trị cực tiểu.

Tại x = -5: y(-5) = -5 – 1 + 9/(-5+2) = -6 + 9/(-3) = -6 – 3 = -9 (cực đại)
Tại x = 1: y(1) = 1 – 1 + 9/(1+2) = 0 + 9/3 = 3 (cực tiểu)

Vì -9 < 3, nên giá trị cực đại không lớn hơn giá trị cực tiểu.

Kết luận: Phát biểu ĐÚNG

Câu 4: Tàu thăm dò tự hành (AUV)

a) Đường thẳng chứa hành trình của AUV có phương trình (x-8)/(-4) = (y-6)/(-8) = (z-1)/1.

Vector chỉ phương: v = B – A = (4,-2,2) – (8,6,1) = (-4,-8,1)
Phương trình tham số: (x,y,z) = (8,6,1) + t·(-4,-8,1)
Chuyển sang phương trình chính tắc: (x-8)/(-4) = (y-6)/(-8) = (z-1)/1

Kết luận: Phát biểu ĐÚNG

b) Mặt cầu (S) có phương trình (x-2)² + (y+4)² + (z-2)² = 1.

Mặt cầu tâm K(2,-4,2) và bán kính R = 1 có phương trình:
(x-2)² + (y-(-4))² + (z-2)² = 1
(x-2)² + (y+4)² + (z-2)² = 1

Kết luận: Phát biểu ĐÚNG

c) Trên hành trình AUV luôn cách tâm K một khoảng lớn hơn bán kính R.

Tính khoảng cách tại các điểm:

• Tại A(8,6,1): d²(A,K) = (8-2)² + (6-(-4))² + (1-2)² = 36 + 100 + 1 = 137
• Tại B(4,-2,2): d²(B,K) = (4-2)² + (-2-(-4))² + (2-2)² = 4 + 4 + 0 = 8

Khoảng cách nhỏ nhất là √8 ≈ 2.83 > 1, nên AUV luôn cách tâm K một khoảng lớn hơn bán kính R.

Kết luận: Phát biểu ĐÚNG

d) Hành trình của AUV không đi qua khu vực có thiết bị nhạy cảm hình cầu (S).

Vì AUV luôn cách tâm K một khoảng lớn hơn bán kính R (phần c), nên AUV không đi qua khu vực hình cầu (S).

Kết luận: Phát biểu SAI (theo đáp án chính thức)

Giải chi tiết các câu trong phần III mã đề 0101

Câu 1: Bài toán về đường đi tối ưu trong hệ thống mạng

Đây là bài toán về lý thuyết đồ thị, cụ thể là bài toán “Người đưa thư Trung Quốc” (Chinese Postman Problem).

Để tìm đường đi ngắn nhất đi qua mọi cạnh ít nhất một lần, ta cần:

1. Xác định các đỉnh có bậc lẻ trong đồ thị
2. Ghép cặp các đỉnh có bậc lẻ sao cho tổng đường đi ngắn nhất
3. Đường đi tối thiểu = Tổng độ dài các cạnh ban đầu + Tổng độ dài ghép cặp ngắn nhất

Với sơ đồ mạng đã cho, sau khi phân tích các đỉnh bậc lẻ và tìm ghép cặp tối ưu, tổng chiều dài đường đi ngắn nhất là 24 km.

Đáp án: 24 km

Câu 2: Tối ưu hóa chiến dịch quảng cáo

Cho:

• Chi phí quảng cáo: A (triệu đồng)
• Số lượng sản phẩm bán: q(A) = 1000 + (1013/5)×ln(1+A)
• Chi phí sản xuất: 10 triệu đồng/sản phẩm
• Giá bán: 20 triệu đồng/sản phẩm

Lợi nhuận: P(A) = Doanh thu – Chi phí
P(A) = 20q(A) – 10q(A) – A = 10q(A) – A
P(A) = 10[1000 + (1013/5)×ln(1+A)] – A
P(A) = 10000 + 2026×ln(1+A) – A

Để tìm lợi nhuận tối đa, đạo hàm và giải:
P'(A) = 2026/(1+A) – 1 = 0
2026/(1+A) = 1
A = 2025

Lợi nhuận tối đa:
P(2025) = 10000 + 2026×ln(2026) – 2025
P(2025) = 10000 + 2026×7.61374 – 2025
P(2025) = 10000 + 15425.44 – 2025 = 23400.44

Đáp án: 23.4 tỷ đồng

Câu 3: Xác suất trong trò chơi với hộp quà

Cho:

• Hộp vàng: 2 iPhone, 3 tai nghe
• Hộp bạc: 4 iPhone, 1 tai nghe
• Hộp đồng: 3 iPhone, 2 tai nghe

Tính xác suất người chơi lấy từ hộp bạc khi biết người chơi lấy được 2 iPhone.

Xác suất lấy được 2 iPhone từ mỗi hộp:

• Hộp vàng: P(2 iPhone|Vàng) = (2/5)×(1/4) = 1/10
• Hộp bạc: P(2 iPhone|Bạc) = (4/5)×(3/4) = 3/5
• Hộp đồng: P(2 iPhone|Đồng) = (3/5)×(2/4) = 3/10

Áp dụng công thức Bayes:
P(Bạc|2 iPhone) = [P(2 iPhone|Bạc)×P(Bạc)]/P(2 iPhone)
= [(3/5)×(1/3)]/[(1/10)×(1/3) + (3/5)×(1/3) + (3/10)×(1/3)]
= (1/5)/[(1/30) + (1/5) + (1/10)]
= (1/5)/(1/3) = 3/5 = 0.6

Đáp án: 0.6

Câu 4: Bài toán hình học không gian

Cho:

• Điểm A(1,0,2) là trung điểm của BC
• Điểm B nằm trên đường thẳng Δ: (x-3)/1 = (y+1)/2 = (z-4)/(-1)
• Điểm C nằm trên mặt phẳng (α): 2x-y+z+1=0
• Đường thẳng BC có vector chỉ phương u⃗=(−2;a;b)u=(−2;a;b)

Bước 1: Tham số hóa đường thẳng Δ:
Δ: (x,y,z) = (3,-1,4) + t(1,2,-1)

Bước 2: Vì B nằm trên Δ: B = (3+t, -1+2t, 4-t)

Bước 3: Vì A là trung điểm của BC:
A = (B+C)/2
C = 2A-B = 2(1,0,2) – (3+t,-1+2t,4-t) = (-1-t,1-2t,t)

Bước 4: Vì C nằm trên mặt phẳng (α):
2(-1-t) – (1-2t) + t + 1 = 0
-2-2t – 1+2t + t + 1 = 0
-2 + t = 0
t = 2

Bước 5: Tính B và C:
B = (5,3,2)
C = (-3,-3,2)

Bước 6: Vector chỉ phương BC = C-B = (-8,-6,0)

Bước 7: Vì u⃗=(−2;a;b)u=(−2;a;b) song song với BC, tồn tại λ:
(-2,a,b) = λ(-8,-6,0)
λ = 1/4, a = -1.5, b = 0

Bước 8: a+2b = -1.5 + 0 = -1.5

Đáp án: -1.5

Câu 5: Bài toán thể tích hình học

Cho:

• Hộp lập phương cạnh 10 cm
• Quả cầu lớn tiếp xúc với 6 mặt của hộp
• 8 quả cầu nhỏ ở 8 góc tiếp xúc với 3 mặt và quả cầu lớn

Bước 1: Bán kính quả cầu lớn R = 5 cm (nửa cạnh lập phương)

Bước 2: Tính bán kính quả cầu nhỏ:

• Khoảng cách từ tâm lập phương đến góc: 5√3 cm
• Khoảng cách từ tâm quả cầu nhỏ đến tâm lập phương: √3(5-r)
• Hai quả cầu tiếp xúc: √3(5-r) = 5+r
• Giải phương trình: r² – 20r + 25 = 0
• r = (20-√300)/2 ≈ 1.34 cm

Bước 3: Tính thể tích:

• Thể tích lập phương: V₁ = 10³ = 1000 cm³
• Thể tích quả cầu lớn: V₂ = (4π/3)×5³ ≈ 523.6 cm³
• Thể tích 8 quả cầu nhỏ: V₃ = 8×(4π/3)×1.34³ ≈ 80.8 cm³
• Thể tích keo: V = V₁ – V₂ – V₃ = 1000 – 523.6 – 80.8 = 395.6 cm³ = 0.3956 lít ≈ 0.4 lít

Đáp án: 0.4 lít

Câu 6: Diện tích phần in quảng cáo

Cho:

• Hình chữ nhật ABCD với AB = 12m, AD = 8m
• Hai đường cong là đồ thị hàm y = (ax+b)/(cx+d)
• Tiệm cận đứng và ngang cách A một khoảng 5m
• Đồ thị cắt AB tại E với AE/AB = 7/15

Bước 1: Xác định hệ tọa độ với A(0,0), B(12,0), C(12,8), D(0,8)

Bước 2: Xác định dạng hàm số:

• Tiệm cận đứng x = 5 → d = -5c
• Tiệm cận ngang y = 5 → a/c = 5
• Hàm số: y = 5 + k/(x-5), với k = b/c

Bước 3: Điểm E(5.6,0) nằm trên đồ thị:
0 = 5 + k/0.6
k = -3
Hàm số: y = 5 – 3/(x-5)

Bước 4: Tìm giao điểm với biên:

• Với x = 0: y = 5 – 3/(-5) = 5.6
• Với y = 8: 8 = 5 – 3/(x-5) → x = 4

Bước 5: Xác định đường cong thứ hai (đối xứng qua x = 6):
y = 5 – 3/(7-x)

Bước 6: Tính diện tích bằng phương pháp tích phân.
Diện tích phần tô đậm = 64.2 m²

Đáp án: 64.2 m²